Il codice agli elementi finiti discontinui di Galerkin (DG) MIGALE nasce dal pioneristico lavoro del Prof. Francesco Bassi (attualmente presso l’Università degli studi di Bergamo) ed è stato continuamente sviluppato negli anni con i contributi di vari gruppi di ricerca universitari. Oltre al gruppo dell’Università degli Studi di Bergamo (F. Bassi, A. Colombo, A. Botti e altri) hanno collaborato allo sviluppo del progetto sia l’Università degli Studi di Brescia (A. Ghidoni, S. Reaby e G. Noventa) sia l’Università della Calabria (C. De Bartolo e A. Nigro) oltre, ovviamene, all’Università Politecnica delle Marche (A. Crivellini e M. Franciolini). Il metodo DG offre diversi vantaggi rispetto ai metodi numerici tradizionalmente impiegati nella Fluidodinamica computazionale. Questo schema numerico, che condivide alcune peculiarità sia con i metodi agli Elementi Finiti (FEM) sia con quelli ai Volumi Finiti (FV), garantisce elevati ordini di accuratezza (più elevati del valore due che è tipico dei software commerciali e open source più diffusi) anche utilizzando reticoli di calcolo di tipo non strutturati fortemente distorti e curvi. Per questa ragione il metodo è particolarmente adatto alla simulazione ad elevata fedeltà dei problemi fluidodinamici tipici dell’ingegneria Industriale, generalmente caratterizzati da geometrie complesse. È anche ritenuto che il metodo possa soppiantare le metodologie numeriche consolidate nei solutori fluidodinamici della prossima generazione. Lo schema numerico è inoltre particolarmente adatto al calcolo parallelo. Tale caratteristica è molto attraente in un’epoca nella quale tutti i sistemi di calcolo, anche quelli per uso personale, sono multi-core e la disponibilità di sistemi di calcolo paralleli distribuiti, quali i Linux Cluster, è sempre più comune. Migale è parallelizzato usando MPI (Message Passing Interface) per le comunicazioni e PETSc per l’algebra lineare, ma ne è stata sviluppata anche una versione basata un approccio ibrido MPI/OpenMP (Open Multi-Processing). Il codice è stato testato, con ottime efficienze parallele, utilizzando fino a 50k cores. Allo stesso tempo il metodo ben si adatta all’utilizzo di tecniche di avanzamento implicite nel tempo. Questi schemi hanno lo scopo di ridurre il tempo computazionale complessivo di una simulazione non stazionaria, sorpassando gli stringenti limiti di stabilità di quelli espliciti. In MIGALE sono stati impiegati con successo, tra gli altri, schemi di tipo Rosenbrock Runge-Kutta che hanno la caratteristica di non richiedere la soluzione di un sistema non lineare e che si sono quindi rivelati particolarmente efficienti. Tuttavia, il metodo richiede ancora di essere ottimizzato dal punto di vista della efficienza computazionale e diverse attività di ricerca hanno avuto come questo scopo, per esempio lo sviluppo di solutori p-multigrid, matrix-free, lo sviluppo di una metodologia di adattività nell’ordine della soluzione etc… La flessibilità del framework numerico di MIGALE ha permesso di sviluppare, utilizzando gli stessi ingredienti numerici, diversi solutori: per flussi comprimibili e incomprimibili; per la simulazione diretta della turbolenza (DNS) e per quella modellata per mezzo delle equazione mediate alla Reynolds (RANS) e modelli di chiusura k-ω e Spalart-Allmaras. Per quanto riguarda la simulazione di flussi turbolenti va segnalato come le proprietà di dissipazione e dispersione numerica proprie rendono il metodo un ottimo candidato per la Implicit Large Eddy Simulation (ILES), approccio per cui solo le strutture turbolente più grandi sono risolte. Dal punto di vista fisico, quest’ultimo approccio ha permesso di studiare con successo diversi flussi transizionali e/o caratterizzati da separazione, ambito nel quale gli approcci standard RANS e LES mostrano alcune difficoltà.
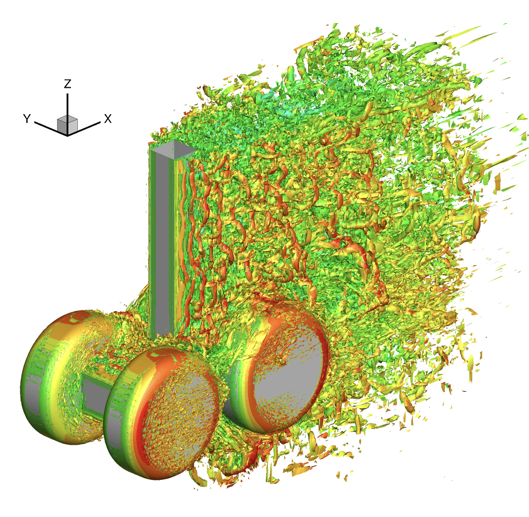
Figura 1: Simulazione DG ILES del flusso attorno ad un carrello di atterraggio, Reynolds 106, iso-superficie di λ2=-1 colorata con la componente x della velocità

Figura 2: Simulazione DG ILES del flusso transizionale su una lastra piana con bordo d’attacco curvo, Reynolds 6900, Tu=2% iso-superficie di λ2=-1 colorata con la componente x della velocità
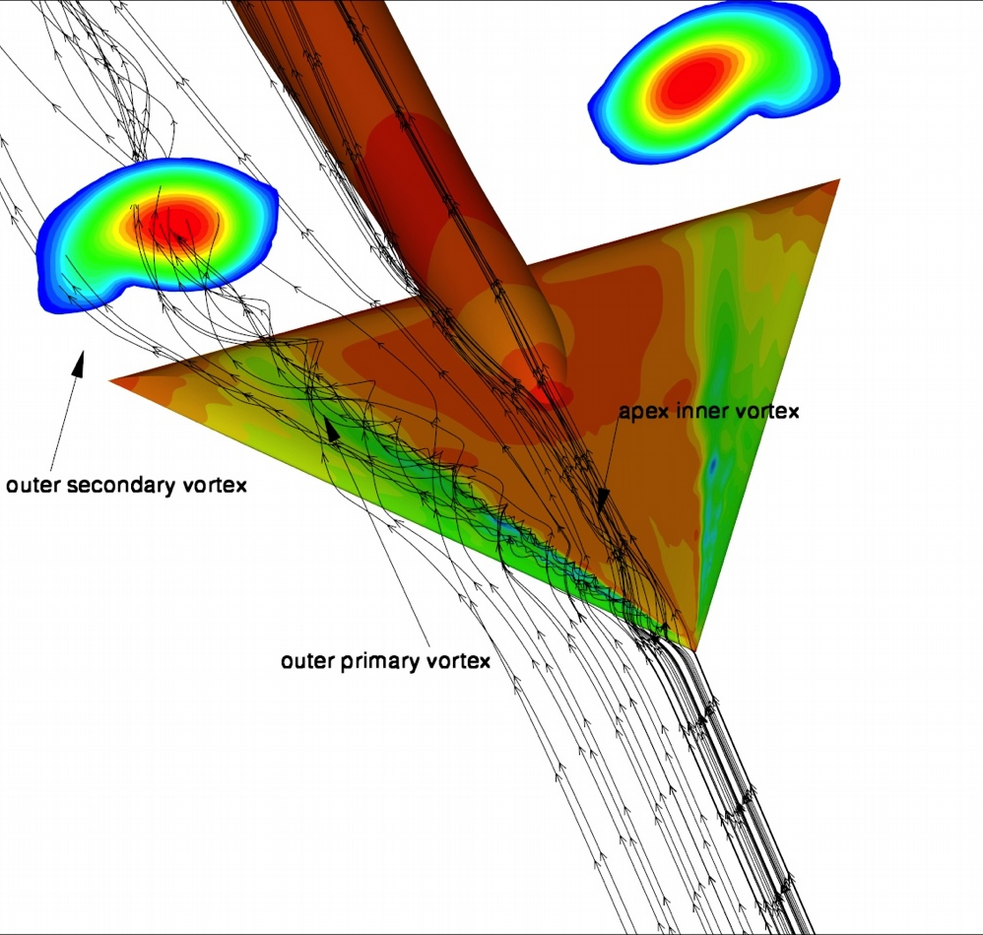
Figura 3: Simulazione DG RANS (modello Spalart-Allmaras) del flusso attorno ad un ala a delta, Reynolds 106, distruzione di cp a parete e contour plot della “eddy viscosity “ in scia.

Figura 4: Simulazione DG DNS del flusso attorno ad una sfera, Reynolds 103, iso-superficie di λ2=-10-3 colorata con il modulo della vorticità della velocità

Figura 5: Simulazione DG bidimensionale della scia a valle di un profilo NACA 0012 in moto oscillante, Reynolds 3∙103, contour plot della vorticità.
[1] F. BASSI, A. CRIVELLINI, S. REBAY, M. SAVINI – “Discontinuous Galerkin solution of the Reynolds averaged Navier Stokes and k- turbulence model equations”, Computers & Fluids, Volume 34, Issues 4-5, May-June 2005, Pages 507-540.
[2] F. BASSI, A. CRIVELLINI, D. A. DI PIETRO, S. REBAY – “An artificial compressibility flux for the discontinuous Galerkin solution of the incompressible Navier–Stokes equations”, Journal of Computational Physics, Volume 218, Issue 2, 1 November 2006, Pages 794-815.
[3] F. BASSI, A. CRIVELLINI, D. A. DI PIETRO, S. REBAY – “An implicit high-order discontinuous Galerkin method for steady and unsteady incompressible flows”, Computers & Fluids, Volume 36, Issue 10, December 2007, Pages 1529-1546.
[4] A. CRIVELLINI, F.BASSI -“An implicit matrix-free Discontinuous Galerkin solver for viscous and turbulent aerodynamic simulations”, Computers & Fluids, Volume 50, Issue 1, November 2011, Pages 81-93
[5] A. CRIVELLINI, V. D’ ALESSANDRO, F.BASSI-“A Spalart–Allmaras turbulence model implementation in a discontinuous Galerkin solver for incompressible flows”, Journal of Computational Physics, Volume 241, 15 May 2013, Pages 388-415
[6] A. CRIVELLINI, V. D’ ALESSANDRO, F.BASSI – “High-order discontinuous Galerkin RANS solutions of the incompressible flow over a delta wing”, 2013, Computers and Fluids 88, Pages. 663 – 677
[7] A. CRIVELLINI, V. D’ ALESSANDRO, “Spalart-Allmaras model apparent transition and RANS simulations of laminar separation bubbles on airfoils”, International Journal of Heat and Fluid Flow, 2014, Volume 47, June Pages 70-83.
[8] F. BASSI, L. BOTTI, A. COLOMBO, A. CRIVELLINI, A. GHIDONI, C. MASSA, “On the development of an implicit high-order Discontinuous Galerkin method for DNS and implicit LES of turbulent flows”, EUROPEAN JOURNAL OF MECHANICS. B, FLUIDS, Volume 55, Part 2, January–February 2016, Pages 367-379.
[9] A. CRIVELLINI, “Assessment of a sponge layer as a non-reflective boundary treatment with highly accurate gust–airfoil interaction results”, INTERNATIONAL JOURNAL OF COMPUTATIONAL FLUID DYNAMICS, Volume 30, 2016 – Issue 2, Pages 176-200.
[10] M. FRANCIOLINI, A. CRIVELLINI, A. NIGRO, “On the efficiency of a matrix-free linearly implicit time integration strategy for high-order Discontinuous Galerkin solutions of incompressible turbulent flows”, COMPUTERS & FLUIDS, Volume 159, 15 December 2017, Pages 276-294.
