The discontinuous finite element code of Galerkin (DG) MIGALE is the result of the pioneering work of Prof. Francesco Bassi (currently at the University of Bergamo) and has been continuously developed over the years with the contributions of various university research groups. In addition to the group of the University of Bergamo (F. Bassi, A. Colombo, A. Botti and others), both the University of Brescia (A. Ghidoni, S. Reaby and G. Noventa) and the University of Calabria (C. De Bartolo and A. Nigro), as well as the Polytechnic University of Marche (A. Crivellini and M. Franciolini) have collaborated in the development of the project. The DG method offers several advantages over the numerical methods traditionally used in computational fluid dynamics field. This numerical scheme, which shares some peculiarities with both Finite Element (FEM) and Finite Volume (FV) methods, guarantees high orders of accuracy (higher than value typical of the most common commercial and open source software) even using unstructured calculation grids that are characterized by strongly distorted and curved elements. For this reason, the method is particularly suitable for high-fidelity simulation of fluid dynamics problems typical of industrial engineering, generally characterized by complex geometries. It is also considered that the method can replace the numerical methodologies consolidated in the next generation of fluid dynamic solvers. The numerical scheme is also particularly suitable for parallel calculation. This feature is very attractive in an age in which all computing systems, even those for personal use, are multi-core and the availability of distributed parallel computing systems, such as Linux Clusters, is increasingly common. MIGALE is parallelized using MPI (Message Passing Interface) for communications and PETSc for linear algebra, but a version based on a hybrid MPI/OpenMP (Open Multi-Processing) approach has also been developed. The code has been tested, with excellent parallel efficiencies, using up to 50k cores. Moreover, the method is well suited to implicit time integration methods. These schemes aim to reduce the overall computational time of a non-stationary simulation, overcoming the strict stability limits of the explicit ones. In MIGALE have been used with success, among the others, Runge-Kutta methods of the Rosenbrock type. These methods, not requiring the solution of a non-linear system, have proved to be particularly efficient. However, the method still requires an optimization from the point of view of the computational efficiency and several research activities have been performed at this purpose. For example, the development of p-multigrid and matrix-free solvers as well as the development of a p-adaptivity algorithm, etc. … The flexibility of MIGALE’s numerical framework has allowed the implementation, using the same numerical ingredients, of different solvers: for compressible and incompressible flows; for the direct simulation of turbulence (DNS) and for the Reynolds averaged equations (RANS) together with a closure model, such as the k-ω or the Spalart-Allmaras. As far as the simulation of turbulent flows is concerned, it should be noted that the dissipation and numerical dispersion properties of the method make it an excellent candidate for Implicit Large Eddy Simulation (ILES). Following this approach only the largest turbulent structures are resolved. From a physical point of view, the later approach allowed to successfully study different transitional flows and/or characterized by separation, a field in which the standard approaches RANS and LES usually show inaccuracies.
The following Linux are available:
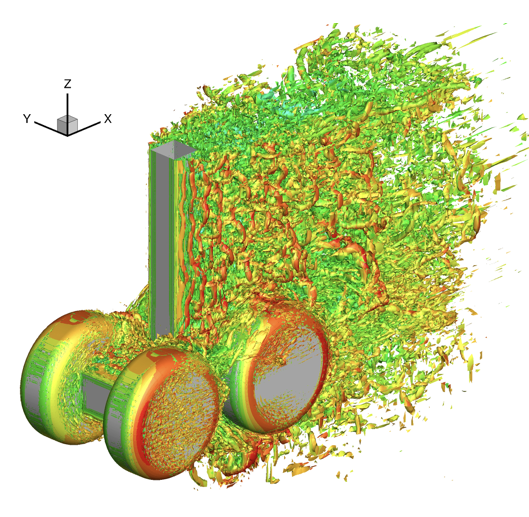
Figure 1: DG ILES simulation of the flow past a landing gear, Reynolds 106, λ2=-1 iso-surface coloured by the x the velocity component.

Figure 2: DG ILES simulation of the transitional flow past a blunt leading edge flat plate, Reynolds 6900 and Tu=2%, λ2=-1 iso-surface coloured by the x the velocity component.

Figure 3: DG RANS simulation (Spalart-Allmaras model) of the flow past a Delta Wing, Reynolds 106, cp distribution on the wing and contour of eddy viscosity on the wake.

Figure 4: DG DNS simulation of the flow past a sphere, Reynolds 6900, λ2=-10-3 iso-surface coloured by the x the vorticity magnitude.

Figure 5: two-dimensional DG simulation of a heaving NACA 0012 profile, Reynolds 3∙103, contour plot of the vorticity.
[1] F. BASSI, A. CRIVELLINI, S. REBAY, M. SAVINI – “Discontinuous Galerkin solution of the Reynolds averaged Navier Stokes and k- turbulence model equations”, Computers & Fluids, Volume 34, Issues 4-5, May-June 2005, Pages 507-540.
[2] F. BASSI, A. CRIVELLINI, D. A. DI PIETRO, S. REBAY – “An artificial compressibility flux for the discontinuous Galerkin solution of the incompressible Navier–Stokes equations”, Journal of Computational Physics, Volume 218, Issue 2, 1 November 2006, Pages 794-815.
[3] F. BASSI, A. CRIVELLINI, D. A. DI PIETRO, S. REBAY – “An implicit high-order discontinuous Galerkin method for steady and unsteady incompressible flows”, Computers & Fluids, Volume 36, Issue 10, December 2007, Pages 1529-1546.
[4] A. CRIVELLINI, F.BASSI -“An implicit matrix-free Discontinuous Galerkin solver for viscous and turbulent aerodynamic simulations”, Computers & Fluids, Volume 50, Issue 1, November 2011, Pages 81-93
[5] A. CRIVELLINI, V. D’ ALESSANDRO, F.BASSI-“A Spalart–Allmaras turbulence model implementation in a discontinuous Galerkin solver for incompressible flows”, Journal of Computational Physics, Volume 241, 15 May 2013, Pages 388-415
[6] A. CRIVELLINI, V. D’ ALESSANDRO, F.BASSI – “High-order discontinuous Galerkin RANS solutions of the incompressible flow over a delta wing”, 2013, Computers and Fluids 88, Pages. 663 – 677
[7] A. CRIVELLINI, V. D’ ALESSANDRO, “Spalart-Allmaras model apparent transition and RANS simulations of laminar separation bubbles on airfoils”, International Journal of Heat and Fluid Flow, 2014, Volume 47, June Pages 70-83.
[8] F. BASSI, L. BOTTI, A. COLOMBO, A. CRIVELLINI, A. GHIDONI, C. MASSA, “On the development of an implicit high-order Discontinuous Galerkin method for DNS and implicit LES of turbulent flows”, EUROPEAN JOURNAL OF MECHANICS. B, FLUIDS, Volume 55, Part 2, January–February 2016, Pages 367-379.
[9] A. CRIVELLINI, “Assessment of a sponge layer as a non-reflective boundary treatment with highly accurate gust–airfoil interaction results”, INTERNATIONAL JOURNAL OF COMPUTATIONAL FLUID DYNAMICS, Volume 30, 2016 – Issue 2, Pages 176-200.
[10] M. FRANCIOLINI, A. CRIVELLINI, A. NIGRO, “On the efficiency of a matrix-free linearly implicit time integration strategy for high-order Discontinuous Galerkin solutions of incompressible turbulent flows”, COMPUTERS & FLUIDS, Volume 159, 15 December 2017, Pages 276-294.
